Gaussian Integers are being a Euclidean Domain

I encountered this theorem during my study of ring theory last term. Now, I’ll demonstrate that Gaussian Integers form a Euclidean Domain. Before delving into the proof, let me provide some necessary definitions.

Euclidean Domain

Let D be an Euclidean Domain. Then, D is a comutative ring with 1. D must satisfy the following properties

First define a function, usually it is called norm: \(N: D \rightarrow \mathbb{Z}^{+}\)

If \(a,b \in D\) and \(a \neq 0, b \neq 0\) then \(N(a) \leq N(ab)\)
If \(a,b \in D\) where \(b \neq 0\) there exists \(q, r \in D\) such that \(a = bq + r\) where \(r = 0\) or \(N(r) < N(b)\)

A common example of an Euclidean domain is \(\mathbb{Z}\) with \(N(m) = \vert m \vert\)

Gaussian Integers

Gaussian Integers are a subset of \(\mathbb{C}\). So that means a gaussian integer have real and imaginary parts and those parts are integers. Here is the definition of the set:

\[\mathbb{Z}[i] = \{ a + bi \vert a, b \in \mathbb{Z} \}\]

Now we will define a norm that will work for us.

Define \(N(\alpha) = \alpha \overline{\alpha} = \vert \alpha^{2} \vert\)

Take \(\alpha = a + bi, \overline{\alpha} = a - bi \in \mathbb{Z}[i]\) where \(a,b \in \mathbb{Z}\). Then \(N(\alpha) = a^{2} + b^{2}\)

Then let’s prove the first requirement to be a Euclidean domain.

First Part

We will show that for all \(\alpha, \beta \in \mathbb{Z}[i]\) we have \(N(\alpha) \leq N(\alpha \beta)\).

\[N(\alpha \beta) = \alpha \beta \overline{\alpha \beta} = \alpha \beta \overline{\alpha} \overline{\beta} = \alpha \overline{\alpha} \beta \overline{\beta} = N(\alpha) N(\beta)\]

Since for all \(\alpha \in \mathbb{Z}[i]\) we have \(N(\alpha) \geq 1\). (We have it because of definiton of function N.)

Now, we can say \(N(\alpha) \leq N(\alpha \beta)\).

Second part

Now, we will proceed with showing that for all \(\alpha, \beta \in \mathbb{Z}[i]\), where \(\beta \neq 0\) there exists \(\gamma, \rho \in \mathbb{Z}[i]\) such that \(\alpha = \beta \gamma + \rho\) where \(\rho = 0\) or \(\rho \leq N(\beta)\).

Now, assume \(\alpha = (a + bi), \beta = (c + di)\) then we have \(\beta^{-1} = \frac{(c-di)}{c^{2}+d^{2}} = \frac{\overline{\beta}}{\vert \vert \beta \vert \vert^{2}}\)

Now examine \(\alpha \beta^{-1}\)

\[\alpha \beta^{-1} = \frac{ (a+bi)(c-di) }{c^{2}+d^{2}} = \frac{1}{c^{2}+d^{2}} ( (ac + bd) + (bc-ad)i )\]

\[\hspace{0.1cm} = \frac{(ac+bd)}{c^{2}+d^{2}} + \frac{(bc-ad)}{c^{2}+d^{2}} i\] \[\hspace{0.1cm} = (q_{1} + r_{1}) + (q_{2} + r_{2})i\]

With \(-\frac{1}{2} \leq r_{1}, r_{2} \leq \frac{1}{2}\)

So we can ask, why we have \(q_{1}, r_{1}, q_{2}\) and \(r_{2}?\). The answer is simple we know that \(\frac{(ac+bd)}{c^{2}+d^{2}}\) and \(\frac{(bc-ad)}{c^{2}+d^{2}}\) are rational numbers, more general they are reel numbers since \(a, b, c, d \in \mathbb{Z}\) Then we have this feature:

For any \(x \in \mathbb{R}\), we have

\(x = \lfloor x \rfloor + r_{1}, 0 \leq r_{1} \leq \frac{1}{2}\)

\(x = \lceil x \rceil + r_{2}, -\frac{1}{2} \leq r_{2} \leq 0\)

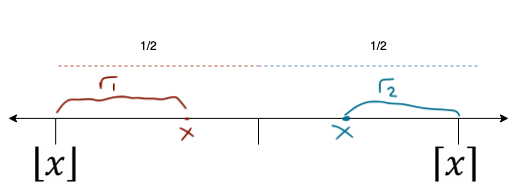
Then finally we can write

\[\alpha \beta^{-1} = (q_{1} + q_{1}i) + (r_{1} + r_{2}i) \Rightarrow \alpha = \beta \underset{\gamma}{\underbrace{(q_{1} + q_{2}i)}} + \underset{\rho}{\underbrace{\beta(r_{1} + r_{2}i)}}\]

\[\alpha = \beta\gamma + \rho\]

Now we find \(\gamma\) and \(\rho\). We just need to show \(\rho = 0\) or \(N(\rho) \leq N(\beta)\).If \(\rho = 0\) is okay. There is nothing to show. Let’s show the second one.

\[N(\rho) = \beta \overline{\beta} (r_{1} + r_{2}i)(r_{1} - r_{2}) = N(\beta) \underset{0 \leq r_{1}^{2} + r_{2}^{2} \leq 1}{ \underbrace{(r_{1}^{2} + r_{2}^{2}})} \leq N(\beta)\]

Hence, \(\mathbb{Z}[i]\) is a Euclidean Domain.

Here is a video about the proof.